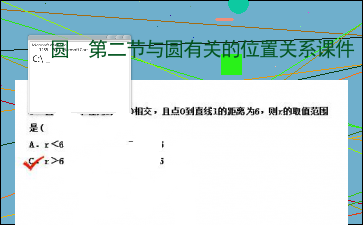
圆 第二节与圆有关的位置关系课件
以下为《圆 第二节与圆有关的位置关系课件》的无排版文字预览,完整内容请下载
第二节 与圆有关的位置关系考点一 点、直线与圆的位置关系
例1 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA,PB与x轴分别交于A,B两点,若点A,点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.81.直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6
C.r>6 D.r≥6考点二 切线的性质与判定
命题角度? 切线的性质
例2 (2018·*_**如图,AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上一点,分别连接CB,CD,∠BCD=60°.
(1)求∠ABD的度数;
(2)若AB=6,求PD的长度.2.如图,BM与⊙O相切于点B,若∠MBA=140°,
则∠ACB的度数为( )
A.40° B.50°
C.60° D.70°3.(2019·*_**如图,AB,CD是⊙O的两条直径,过点C的⊙O的切线交AB的延长线于点E,连接AC, BD.
(1)求证:∠ABD=∠CAB;
(2)若B是OE的中点,AC=12,求⊙O的半径.命题角度? 切线的判定 内容过长,仅展示头部和尾部部分文字预览,全文请查看图片预览。
∵OA=OC,∴∠OCA=∠OAC.
∵OD⊥AB,∴∠OAC+∠AEO=90°,
∴∠OCA+∠FCE=90°,即OC⊥FC,
∴CF与⊙O相切.(2)∵OD⊥AB,AC⊥BD,∴∠AOE=∠ACD=90°.
∵∠AEO=∠DEC,∴∠A=∠D.
∵∠A=22.5°,∴∠COB=45°,∴∠COD=45°.
∵OC⊥CF,∴∠OCF=90°,
∴∠COF=∠CFO=45°,∴CF=DF=EF=CO,
∴DE=AB.
在△DEC和△ABC中,
∴△DEC≌△ABC(AAS),∴AC=CD.考点三 三角形的内切圆
例4 (2018·*_**如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为________.7.(2019·*_**如图,边长为2 的等边△ABC的内切圆的半径
为( )
A.1 B. C.2 D.2核心考点 与切线有关的证明与计算
命题规律分析:百变例题 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.[文章尾部最后300字内容到此结束,中间部分内容请查看底下的图片预览]
以上为《圆 第二节与圆有关的位置关系课件》的无排版文字预览,完整内容请下载
圆 第二节与圆有关的位置关系课件由用户“vane914”分享发布,转载请注明出处- 最新版人教版七年级数学下册典型试题汇总
- (初稿1)圆有关问题专练
- 第1章 平行线(知识点组合卷XXXXX浙教7下)
- 第1章 平行线(知识点组合卷XXXXX浙教7下)
- (完整版)人教版七年级数学相交线与平行线证明题专项训练
- 第1章 平行线(知识点组合卷XXXXX浙教7下)
- 第1章 平行线(知识点组合卷XXXXX浙教7下)
- 第1章 平行线XXXXX知识点组合卷XXXXX浙教7下XXXXX
- 第1章 平行线XXXXX知识点组合卷XXXXX浙教7下XXXXX
- 第1章 平行线XXXXX知识点组合卷XXXXX浙教7下XXXXX
- 第1章 平行线XXXXX知识点组合卷XXXXX浙教7下XXXXX
- 第1章 平行线(知识点组合卷XXXXX浙教7下)
- 第1章 平行线(知识点组合卷XXXXX浙教7下)
- 2.1直线与圆的位置关系(2)教学设计
- 题型集训(1)——与圆有关的计算和证明
- 8.9切线长定理练习
- 最新人教版七年级下册数学各章知识点及练习题
- 中考数学复习专练第三轮冲刺专题复习 圆--综合练习题