第1课时 可化为一元一次方程的分式方程课件
以下为《第1课时 可化为一元一次方程的分式方程课件》的无排版文字预览,完整内容请下载
1.5 可化为一元一次方程的分式方程第1课时 可化为一元一次方程的分式方程学习目标:
1、掌握分式方程的概念;
2、理解分式方程的解题思路;
3、初步掌握解分式方程的一般步骤;
4、了解分式方程产生增根的原因及掌握验根的方法. 尹老师今年的年龄与9的差除以她年龄与9的和的商等于—,请同学们猜猜尹老师的年龄.解 :设尹老师的年龄为 x 岁, 列方程得12 概括:
分母中含有未知数的方程,叫作分式方程.此方程有何特征?议一议解分式方程: 化简,得整式方程 2(x-9)=x+9解整式方程,得 x= 27. 把x=27代入最简公分母2(x+9) ∴ 原方程的根是 x = 27.● ● ● ● ●① ② ③检验:得 2(x+9) · ·2(x+9)解:方程两边同乘最简公分母
得整式方程
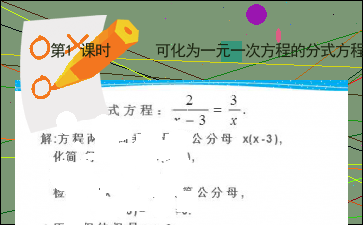
< 内容过长,仅展示头部和尾部部分文字预览,全文请查看图片预览。 x=9, 代入最简公分母,
x(x-3)= 54 ≠0.
∴原方程的根是x= 9.
例2 解分式方程:解:方程两边同乘以最简公分母 2(x-1) 解得 x= 检验: 把x= 代入最简公分母,
2(x-1)= ≠0∴ 原方程的根是 x = 1、在方程的两边同乘各个分式的最简公分母,将原方程化为一元一次方程.
2、解这个一元一次方程.
3、检验:把一元一次方程的解代入最简公分母中,若它的值不等于0,则这个解是原分式方程的根;若它的值等于0,则原分式方程无解.
4、写出原分式方程的根.一化二解三验四写根解可化为一元一次方程的分式方程的基本步骤解分式方程容易犯的错误有:(1)去分母时,原方程的整式部分漏乘.(2)约去分母后,分子是多项式时, 要注意添括号.(因分数线有括号的作用) (3)增根不舍掉. 1.解分式方程:(1)(2)(3)x=3x=-42.解分式方程:谢谢![文章尾部最后300字内容到此结束,中间部分内容请查看底下的图片预览]
以上为《第1课时 可化为一元一次方程的分式方程课件》的无排版文字预览,完整内容请下载
第1课时 可化为一元一次方程的分式方程课件由用户“hanjingyi002”分享发布,转载请注明出处